Math, The Way it Should Be (Unit 2.1: Introduction to Angles)

I've had a hard time figuring out quite how to approach this subject.  It's not my favorite but it sets up a lot of important things that are coming in the future.  All right... here come angles.

So we know how to measure lots of things.  Lengths come in inches, miles, angstroms, meters; time comes in seconds, hours, decades; but in what units do we measure angles?  There are a few options: degrees (the most common), gradians, and radians are a few examples.  If you did your homework from Lesson 1.3, degrees will be news to you.  If you didn't, that's okay.  Units are always arbitrary and the majority of units for angles are also kind of dumb.  So forget about everything but radians.

Why radians?  They're a little trickier at the beginning, but once you get up to speed radians make everything easier.  Let's start with a circle.  How many radians are there in a circle? That's simple! There are this many: \(2\pi\)*.  I usually forget (temporarily) about the \(\pi\) and think about radians in terms of half circles.

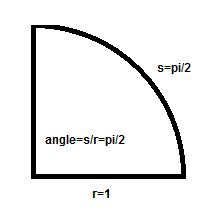
Why that many?  That's a trickier question.  It has to do with the interior angle of a portion of a circle being the ratio of the radius to the arc length.  If you understood that last sentence, it all makes sense given that the circumference of a circle of a given radius is \(2r\pi\).  If not, here's an example.  Say you have one quarter of a circle and you want to know what the interior angle is.  The arc (that's the curvy part) length is \(\frac{\pi}{2}\) (one quarter of the full circle or \(2\pi\frac{1}{4}\ = \frac{\pi}{2}\)). and the radius is 1 (for my own convenience).  We then take the ratio, or \(\frac{\pi}{2*1}\) and that is our angle.  It's pretty nice that for a circle with \(r = 1\) the interior angle is the same as the arc length.

Once you have this concept down, the rest is easy.  Digest the concept of radians and always remember that for a circle with \(r = 1\) the angle in radians is equal to the arc length and you will be golden, provided you can figure out the arc length.  Just figure out what fraction of the full circle it is and multiply that fraction by \(2\pi\).

Homework:

• Continue forgetting about degrees.
• Start slipping your new radian knowledge into everyday conversation.
• Look for triangles, because that's where we're headed next.

-Lane

*If you notice, the math is a bit fancier.  That's because in addition to the changing background picture, I have also added the ability to type math in using LaTeX commands.  I'm new to this format so it will take me a little longer to write posts but the material lends itself to shorter posts so we can move through this a little more quickly anyways.