As you (probably) well know, the final lesson in each unit includes a summary of previous lessons and then some personal philosophy from me. But before we get to that, I would like to point anyone new to this series to the first post in the series. I usually also link to the first lesson in the unit, but I'll be getting to that soon enough.
So this unit was pretty much a refresher on geometry and a little bit of what is usually covered in trigonometry classes. We started with the very of geometry, angles. The most important thing to take away from that lesson is how radians work. They're not the most intuitive but once you get used to them, they're well worth it, as you will see later. After angles came triangles. The most important thing to remember about those three-sided shapes is that they're the key to doing all kinds of things with vectors. In fact, you can make an infinite number of triangles with a given vector... it's choosing the right one that is difficult (and the right triangle is usually right!). Then we covered functions that are basically little machines that turn one thing into another thing. Trigonometry rounded out July. The take-away message there regarded the trigonometric functions (most importantly: sine, cosine, and tangent). The penultimate lesson dealt with areas and volumes. I wasn't very happy with that lesson but I consider that most of geometry education deals with memorization of formulas that becomes largely obsolete with an understanding of calculus, so I kind of glossed over it, (hopefully) leaving you with exactly enough to understand some of the things that come next.
So here's the philosophy: I don't really like geometry or trigonometry. My real interests lie elsewhere in mathematics. Unfortunately, like all of mathematics, those more interesting areas are built on the foundation provided by less complex mathematics, specifically algebra and geometry. So even though I don't like them, I have realized that they are necessary to fundamentally understand what is going on in more complex operations. To me, things like geometry and the multiplication tables are like the alphabet: they're not that interesting in and of themselves, but combine them together and you can form the words that describe the whole universe in a way that very few people understand.
-Lane
Showing posts with label Math. Show all posts
Showing posts with label Math. Show all posts
Wednesday, August 10, 2011
Tuesday, August 2, 2011
Math, The Way it Should Be (Unit 2.5: Areas and Volumes)
As usual for this series, if you haven't seen them before, you should check out the first post in the series and the first post in the unit. This unit has kind of stretched on a lot longer than I intended but it is an important one because although I'm not a big fan of geometry and trigonometry, it does set up one of my favorite topics, calculus. In light of that, we'll have this lesson and a summary and then I want to tie up some loose ends and then we'll get to the fun stuff, though perhaps not in the way you might think.
The first thing to be covered right now is the area. Consider the old, familiar Cartesian plane:
Now imagine drawing a shape on this plane. It would have two dimensions. When we talked about vectors, we talked about their length, that is, the "space" that they take up in one dimension. When we want to talk about the "space" taken up in two dimensions, we call it the area. Many regular shapes have special formulas to help figure out their areas and in the interest of brevity, I will allow the reader to tackle that on his or her own. What shapes really interest me right now are rectangles and circles. The reason is because you can make any shape with small enough rectangles or circles. This may not be obvious but trust me, I will explain later.
Circles (more on them here) have an area proportional to the square of their radius:
Rectangles (4-sided, closed shapes with all right angles) have an area equal to the product of the length of their sides:
The first thing to be covered right now is the area. Consider the old, familiar Cartesian plane:
Now imagine drawing a shape on this plane. It would have two dimensions. When we talked about vectors, we talked about their length, that is, the "space" that they take up in one dimension. When we want to talk about the "space" taken up in two dimensions, we call it the area. Many regular shapes have special formulas to help figure out their areas and in the interest of brevity, I will allow the reader to tackle that on his or her own. What shapes really interest me right now are rectangles and circles. The reason is because you can make any shape with small enough rectangles or circles. This may not be obvious but trust me, I will explain later.
Circles (more on them here) have an area proportional to the square of their radius:
\(A = \pi r^2\)
I will prove this to you later, I promise, for now, just please believe me.
Rectangles (4-sided, closed shapes with all right angles) have an area equal to the product of the length of their sides:
\(A = ab\)
Where \(a\) and \(b\) are the lengths of the two adjacent sides. This makes a lot of sense if you go back to the explanation of multiplication earlier in the series.
Volume is the amount of space an object takes up in three dimensions. Again, regular shapes have their own special formulas, which you can find in a number of places on the internet. For volumes, I basically only care about the three-dimensional analog of the rectangle, which is the prism. It is has all right angles and six faces, all of which are rectangles. In essence, the prism is a box and the volume of the box is as follows:
\(V = abc\)
Where \(a\), \(b\), and \(c\) are the lengths of the three sides that are perpendicular to each other.
So those are the basics of areas and volumes. I didn't spend a whole lot of time on them because I really think that memorizing a bunch of formulas for all sorts of shapes isn't very useful because you can just reconstruct them if you know the formulas for rectangles, circles, and prisms and just one other thing (just wait for unit 4!)
Homework: No homework for this lesson because I'm a) feeling benevolent and b) want to go to bed.
-Lane
Thursday, July 21, 2011
Math, The Way it Should Be (Unit 2.4: Trigonometry)
It's been a while since the last math post but that's an important one for this lesson, so if you missed it go ahead back and check it out. As usual, the first post in the whole series is here and the first post in this unit is here. This post is going to be a very brief overview of trigonometry. This is usually a subject covered over the course of a semester so it would be rather silly to try to cover the whole thing in one post so you'll get the highlights. There's going to be a lot in this lesson. Ready?
First off, trigonometry is basically the study of triangles. Remember those? There is a basic refresher here. It also talks a bit about radians which will be really important now and are covered in the first post of the unit (link in the first paragraph). Now there are some special functions that come about in trigonometry and they're aptly named, the trigonometric functions. The first three are fairly basic: the sine, the cosine, and the tangent functions. They are usually seen like this: \(sin(x)\), \(cos(x)\), and \(tan(x)\). What do they do? Well they map the angles to ratios. Let's look at the triangle we had last lesson:
In this case, let's say that the letters represent the length of the sides and they can also serve as the side's name. Let's also label the angles (the names will also represent the measure of that angle in radians):
Now we're in business. When we start with trigonometry, we usually start with a right triangle. Therefore, let's assume that \(Y = \frac{\pi}{2}\). This angle won't factor heavily into the discussion but this is an important step to take. Now, let's put these definitions to work defining the trigonometric functions. The sine function takes a given angle and spits out the ratio of the opposite side to the hypotenuse of a hypothetical triangle with that angle. For example, \(sin(Z) = \frac{a}{c}\). In the same way, \(sin(X) = \frac{b}{c}\).
The cosine function is equally easy. It takes the angle and spits out the ratio of the adjacent side and the hypotenuse. In this case, \(cos(X) = \frac{a}{c}\) and \(cos(Z) = \frac{b}{c}\). The observant reader will notice that \(cos(X) = sin(Z)\) and this will always be true for any two positive angles that add up to \(\frac{\pi}{2}\). You'll also notice that \(sin(X) = cos(Z)\) and the exact same logic applies. This is not necessarily true for all angles as the functions are extended to all real and complex angles!
The last of the basic trigonometric functions is the tangent function. It returns the ratio of the two legs of the triangle (in other words, the two sides that aren't the hypotenuse). \(tan(X) = \frac{b}{a}\) and \(tan(Z) = \frac{a}{b}\). And there you have it, the first three trigonometric functions. They are the ones that are seen most often.
What about the others? There are many many many. The next three return the inverse of their basic counterpart:
secant:
\(sec(x) = \frac{1}{cos(x)}\)
cosecant:
\(csc(x) = \frac{1}{sin(x)}\)
cotangent:
\(cot(x) = \frac{1}{tan(x)}\)
The last ones that I'm going to cover now are the inverse trigonometric functions. They basically take the ratio of two sides of a triangle and return an angle. In other words they do the opposite of their inverse,
\(Sin^{-1}(\frac{a}{c}) = Z\)
\(Cos^{-1}(\frac{a}{c}) = X\)
\(Tan^{-1}(\frac{a}{b}) = Z\)
These functions go by many names, but the ones I hear most often sound like "inverse tangent" or "arcsine". Just stick either an inverse or an "arc" in front of the original function name and you're good to go! That's all for now on trigonometry. The potential homework here is enormous (there is a lot of fun you can have playing with trigonometric functions).
Homework:
First off, trigonometry is basically the study of triangles. Remember those? There is a basic refresher here. It also talks a bit about radians which will be really important now and are covered in the first post of the unit (link in the first paragraph). Now there are some special functions that come about in trigonometry and they're aptly named, the trigonometric functions. The first three are fairly basic: the sine, the cosine, and the tangent functions. They are usually seen like this: \(sin(x)\), \(cos(x)\), and \(tan(x)\). What do they do? Well they map the angles to ratios. Let's look at the triangle we had last lesson:
In this case, let's say that the letters represent the length of the sides and they can also serve as the side's name. Let's also label the angles (the names will also represent the measure of that angle in radians):
The cosine function is equally easy. It takes the angle and spits out the ratio of the adjacent side and the hypotenuse. In this case, \(cos(X) = \frac{a}{c}\) and \(cos(Z) = \frac{b}{c}\). The observant reader will notice that \(cos(X) = sin(Z)\) and this will always be true for any two positive angles that add up to \(\frac{\pi}{2}\). You'll also notice that \(sin(X) = cos(Z)\) and the exact same logic applies. This is not necessarily true for all angles as the functions are extended to all real and complex angles!
The last of the basic trigonometric functions is the tangent function. It returns the ratio of the two legs of the triangle (in other words, the two sides that aren't the hypotenuse). \(tan(X) = \frac{b}{a}\) and \(tan(Z) = \frac{a}{b}\). And there you have it, the first three trigonometric functions. They are the ones that are seen most often.
What about the others? There are many many many. The next three return the inverse of their basic counterpart:
secant:
\(sec(x) = \frac{1}{cos(x)}\)
cosecant:
\(csc(x) = \frac{1}{sin(x)}\)
cotangent:
\(cot(x) = \frac{1}{tan(x)}\)
The last ones that I'm going to cover now are the inverse trigonometric functions. They basically take the ratio of two sides of a triangle and return an angle. In other words they do the opposite of their inverse,
\(Sin^{-1}(\frac{a}{c}) = Z\)
\(Cos^{-1}(\frac{a}{c}) = X\)
\(Tan^{-1}(\frac{a}{b}) = Z\)
These functions go by many names, but the ones I hear most often sound like "inverse tangent" or "arcsine". Just stick either an inverse or an "arc" in front of the original function name and you're good to go! That's all for now on trigonometry. The potential homework here is enormous (there is a lot of fun you can have playing with trigonometric functions).
Homework:
- Prove that for any \(x\), \(sin^{2}(x) + cos^{2}(x) = 1\). (Hint: try starting with the pythagorean theorem).
- Convince yourself that for any \(x\), \(\frac{cos(x)}{sin(x)} = tan(x)\).
- Convince yourself that \(sin(\frac{\pi}{2}-x) = cos(x)\)
-Lane
Wednesday, July 6, 2011
Math, The Way it Should Be (Unit 2.3: Functions)
As per usual, this is the latest (and late, sorry) installment of the Math, The Way it Should Be series. The first post explaining what the point is exists here. The first unit is here and the beginning of this unit is here. This unit is all about functions which are pretty cool objects. Basically, they're boxes that you can put something into and it gives you something else. Functions are important because if you put the same thing into it twice, you'll always get exactly the same thing back out. We say that a function maps a domain to a range:
The domain is all of the things that can go into the function and the range is all of the possible things that can come out. They don't necessarily have to be the same size. We'll come back to this in a second. But first, how do we write a function? Usually it looks a little like this:
The domain is all of the things that can go into the function and the range is all of the possible things that can come out. They don't necessarily have to be the same size. We'll come back to this in a second. But first, how do we write a function? Usually it looks a little like this:
\(f(x)\)
The function's name is "f of x" though the x is just a place-holder, really. To fully define a function, we say what it is and then what its domain is, though this is sometimes omitted when the domain is all numbers. For example, we could define f this way:
\(f(x)=x^2\)
\( -2 {\leq} x {\leq} 2 \)
This means that whatever goes into f gets squared and only numbers between -2 and 2 may be put into f. To find out what happens when we put 1 into f, we just write \(f(1)\) and then carry out the function on 1. We then have:
\(f(1)=1\)
So we know what the function is and it's domain. What about it's range? The best way to figure this out is to graph the function. How do you do that? Recall the lesson where I introduced the Cartesian plane and said that anything could be put on either axis? In this case, you put the domain on one axis and the function on the other, like this:
The red line represents the function values. To find \(f(x)\), just find x on the horizontal axis and then draw a line up to the red line and then over to the vertical axis. You then have your value. To make a graph like this, you just come up with a couple examples and write them into pairs in the form \((x, f(x))\) and then put them on the plane. If you don't remember how to do this, please see the lesson in the link above. Finally, draw a line through the points and you have your function. We can now find out what the range of the function is. The range is the collection of all of the possible outcomes of the function. In this case, you can see that the lowest value is 0 and the highest value is 4. So the range is \(0 {\leq} x {\leq} 4\). And that's all you need to know about functions (for right now)!
Homework:
- Practice with functions. Start thinking of things in terms of functions and then think about graphing them. For example, position as a function of time (\(x(t)\)). Think about what the domain and range might be. Only one assignment for this lesson!
-Lane
Tuesday, June 21, 2011
Math, The Way it Should Be (Unit 2.2: Triangles)
Here comes another math lesson! It's all about triangles, probably one of the most important shapes. However, if you're running a bit behind or are new to the series, you kind find the introductory post here, the start of the first unit is here, and the start of this unit can be found here. While most of that information is not super necessary to today's lesson, not knowing it will prove problematic later.
Now, about triangles. On the face, there's not much to say about them. They have three angles (hence the name) and have three sides. They are closed shapes and always convex, meaning if you put a rubber band around them it would always touch the sides (and all angles are always less than \(\pi\) radians). In fact, the angles always add up to \(\pi\) radians (if you're wondering why I haven't mentioned degrees, go here). This is all well and good, but why are these shapes so important that they get their own lesson?
It's because a special type of triangle, called the right angle, is super important when it comes to splitting up vectors. But before we get to that, let's talk about three kinds of triangles. The first type is acute with all angles less than \(\frac{\pi}{2}\), the second type is obtuse with one angle greater than \(\frac{\pi}{2}\), and the last type is the aforementioned right angle with one angle at exactly \(\frac{\pi}{2}\). These right triangles have a very special property: the sum of the squares of the two sides containing the right angle is equal to the square of the third side (known as the hypotenuse). This is known as the Pythagorean Theorem and more formally looks like this: \(a^2 + b^2 = c^2\)
This is the whole point of the lesson. I don't know if I have mentioned this before, but geometry isn't my favorite part of mathematics so I'm kind of glossing over it to get to the cool stuff. But how does this relate to anything that could possibly be cool? Recall the graph we made in Lesson 1.6 regarding apples and oranges? If you don't, it looked like this:
This graph shows a fruit vector representing a person who has two apples and three oranges. The vector is affectionately known as (2,3). What if we want to know how far away this person is from a person with no fruit at all? We can't just add the apples and oranges because that adds to five and it's pretty obvious that the shortest path between the two points isn't that long. But you can see that the apple vector and the orange vector form a right angle with the fruit vector forming the hypotenuse of a right triangle. We then apply the Pythagorean Theorem:
\(a^2 + b^2 = c^2\)
\(a = 2\)
\(b = 3\)
\(c^2 = 2^2 + 3^2\)
\(c^2 = 4 + 9 = 13\)
\(c = \sqrt{13}\)*
We now know that the length of the fruit vector is equal to \(\sqrt{13}\). Aren't you glad we learned about irrational numbers? Other things to know about the Pythagorean Theorem:
- It can be extended to any number of dimensions (even just one!). All one needs to do to find the length of a vector is to square all of the components and then take the square root.
- It is never described by the term "to Pythagorean" which means "to speculate in the style of Pythagoras". This is a common misconception among engineering students.
- It only applies when applied correctly. The square of the two smaller sides equals the square of the third side. It doesn't work in any other combination. It also only works for right triangles.
- This is a very important thing to remember when we get to trigonometric functions. Keep it in mind.
- Any three integers that can be arranged as a, b, and c and satisfy this relationship are known as "Pythagorean Triples". The most common is 3, 4, and 5. The one I remember best is known as the "Alexander Triple", named for my high school geometry teacher: 20, 21, 29.
This lesson is running long so here's your homework:
- Revisit the lesson on vectors and number lines with this new information in mind.
- Apply the Pythagorean Theorem in one, two, and three dimensions and convince yourself that it's true. If that doesn't do it for you, think of a proof. This problem can be approached through geometry, algebra, or calculus.
-Lane
*The astute student will notice the lack of the \(\pm\) sign in this problem. If you did, good. If you didn't, that's okay but this is a super important point. You almost always need to include it. However, in this case we can reject the negative answer because distances are positive and a negative length is what we call a "non-physical" solution. Math is a powerful tool but sometimes it tells us things that are impossible. Learning to know when math is speaking nonsense and not listening is an important skill that requires critical thinking and common sense.
Thursday, June 16, 2011
Math, The Way it Should Be (Unit 2.1: Introduction to Angles)
I've had a hard time figuring out quite how to approach this subject. It's not my favorite but it sets up a lot of important things that are coming in the future. All right... here come angles.
So we know how to measure lots of things. Lengths come in inches, miles, angstroms, meters; time comes in seconds, hours, decades; but in what units do we measure angles? There are a few options: degrees (the most common), gradians, and radians are a few examples. If you did your homework from Lesson 1.3, degrees will be news to you. If you didn't, that's okay. Units are always arbitrary and the majority of units for angles are also kind of dumb. So forget about everything but radians.
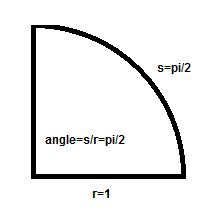
Why radians? They're a little trickier at the beginning, but once you get up to speed radians make everything easier. Let's start with a circle. How many radians are there in a circle? That's simple! There are this many: \(2\pi\)*. I usually forget (temporarily) about the \(\pi\) and think about radians in terms of half circles.
Why that many? That's a trickier question. It has to do with the interior angle of a portion of a circle being the ratio of the radius to the arc length. If you understood that last sentence, it all makes sense given that the circumference of a circle of a given radius is \(2r\pi\). If not, here's an example. Say you have one quarter of a circle and you want to know what the interior angle is. The arc (that's the curvy part) length is \(\frac{\pi}{2}\) (one quarter of the full circle or \(2\pi\frac{1}{4}\ = \frac{\pi}{2}\)). and the radius is 1 (for my own convenience). We then take the ratio, or \(\frac{\pi}{2*1}\) and that is our angle. It's pretty nice that for a circle with \(r = 1\) the interior angle is the same as the arc length.
So we know how to measure lots of things. Lengths come in inches, miles, angstroms, meters; time comes in seconds, hours, decades; but in what units do we measure angles? There are a few options: degrees (the most common), gradians, and radians are a few examples. If you did your homework from Lesson 1.3, degrees will be news to you. If you didn't, that's okay. Units are always arbitrary and the majority of units for angles are also kind of dumb. So forget about everything but radians.
Why radians? They're a little trickier at the beginning, but once you get up to speed radians make everything easier. Let's start with a circle. How many radians are there in a circle? That's simple! There are this many: \(2\pi\)*. I usually forget (temporarily) about the \(\pi\) and think about radians in terms of half circles.
Why that many? That's a trickier question. It has to do with the interior angle of a portion of a circle being the ratio of the radius to the arc length. If you understood that last sentence, it all makes sense given that the circumference of a circle of a given radius is \(2r\pi\). If not, here's an example. Say you have one quarter of a circle and you want to know what the interior angle is. The arc (that's the curvy part) length is \(\frac{\pi}{2}\) (one quarter of the full circle or \(2\pi\frac{1}{4}\ = \frac{\pi}{2}\)). and the radius is 1 (for my own convenience). We then take the ratio, or \(\frac{\pi}{2*1}\) and that is our angle. It's pretty nice that for a circle with \(r = 1\) the interior angle is the same as the arc length.
Once you have this concept down, the rest is easy. Digest the concept of radians and always remember that for a circle with \(r = 1\) the angle in radians is equal to the arc length and you will be golden, provided you can figure out the arc length. Just figure out what fraction of the full circle it is and multiply that fraction by \(2\pi\).
Homework:
- Continue forgetting about degrees.
- Start slipping your new radian knowledge into everyday conversation.
- Look for triangles, because that's where we're headed next.
-Lane
*If you notice, the math is a bit fancier. That's because in addition to the changing background picture, I have also added the ability to type math in using LaTeX commands. I'm new to this format so it will take me a little longer to write posts but the material lends itself to shorter posts so we can move through this a little more quickly anyways.
Saturday, June 11, 2011
Math, the Way it Should Be (Unit 1.6: Summary and a bit of Philosophy)
The last lesson in each unit will go quickly over what was covered in the lessons of the unit and then give some insight into what’s going on in my head with regards to mathematics. In the Lesson 1.1, we covered addition, subtraction, the signs indicating less than and greater than, and the counting numbers. In Lesson 1.2 we added zero and the negative numbers to form the integers as well as covering multiplication and some instances of division. In Lesson 1.3, we learned about the rational numbers, allowing us to carry out division with all integers as well as reviewing addition and multiplication of fractions. In Lesson 1.4, exponents and roots were introduced, leading to the definition of irrational and complex numbers. Finally, in Lesson 1.5, the number line and Cartesian plane were introduced as well as some basic vectors and vector operations. More will come on these topics later.
The first piece of philosophy regarding the education of mathematics that I will share regards the treatment of “word problems”. In my opinion, word problems are demonized by students everywhere because the way they are taught (or at least, taught to me) requires a step of memorization. For example, when I was taking my second algebra class in high school, we covered “solution problems” (problems where two or more liquids were combined in a mixture) in great depth (no pun intended). The teacher I had was a great teacher, but we were taught that every time we encountered a solution problem, we would solve it using the same steps every time. While this worked for the exact type of problems we faced in class, I feel like this isn’t the best way to solve problems. Since I learned to approach problems like an engineer, I have started building equations from the problems. For a new problem, I either create new equations based on what I know about the problem or use a couple, very basic equations (relatively speaking) that I then tailor to the problem. I use the second approach for complex engineering problems, but the first approach is appropriate for almost all problems faced by high school and underclassmen in college.
I will likely not cover any word problems until later, when I plan on dedicating an entire unit to learning how to do every kind of word problem possible. Like many things, however, it will require lots of practice to master and experience is something you can’t get on the internet.
-Lane
-Lane
Monday, June 6, 2011
Solving Partial Differential Equations with Excel
To begin with, this post is not a part of the "Math, the Way it Should Be" series. Although it is a post filled with mathy-goodness, the mathematics involved here are far and away more complex than what I've presented so far in that series. If you're inclined to think things are nerdy, you'll probably think this is pretty nerdy. That being said, let's begin with a short introduction and then I'll tell you what I did.
For complicated differential equations, we have three options for finding a solution. In some cases, the solution may be found analytically but under some circumstances this may involve infinite series to match boundary and/or initial values. The second option is to look up a solution that someone else may have come up with. This approach has limitations as well as not every problem has already been solved by someone else. This leads us to our third option, a numerical solution. The limitations here are that there is always error (analytical solutions are usually exact), serious computing power can be required (I like to use MATLAB), and the last problem is that the user really has to know what he or she is doing in order to avoid unphysical or unrealistic solutions. If you can get past these, however, you are on your way to a powerful tool. Using the following steps, I used Microsoft Excel 2007 to solve the following problem (Laplace's Equation with mixed boundary conditions):
This can now be entered into the domain. Start in the upper left corner. The proper entry (in this case) should be "=0.25*(E2+E4+D3+F3)". Then take the black box in the lower corner of the selected cell and drag this equation across the domain. Then do this again with the whole row, only drag downwards to cover the entire domain. Watch as Excel iterates through and solves the equation over the domain!
For complicated differential equations, we have three options for finding a solution. In some cases, the solution may be found analytically but under some circumstances this may involve infinite series to match boundary and/or initial values. The second option is to look up a solution that someone else may have come up with. This approach has limitations as well as not every problem has already been solved by someone else. This leads us to our third option, a numerical solution. The limitations here are that there is always error (analytical solutions are usually exact), serious computing power can be required (I like to use MATLAB), and the last problem is that the user really has to know what he or she is doing in order to avoid unphysical or unrealistic solutions. If you can get past these, however, you are on your way to a powerful tool. Using the following steps, I used Microsoft Excel 2007 to solve the following problem (Laplace's Equation with mixed boundary conditions):
 |
| Note: y ranges between 0 and 5 and x ranges between 0 and 10 |
The first step is to set up Excel: The first step is to allow Excel to iterate on cells with circular references. This is done by first clicking on the round Microsoft Office button in the upper left-hand corner and selecting "Excel Options". Click on the "Formulas" tab. You will see this:
Click the box enabling reiteration. Set the maximum iterations to 32767 (this is the maximum number) and reduce the maximum change to the desired level of accuracy. I like 0.0000001 for this application.
The next step is to prepare your domain. This is done in the workbook itself. I will be using 0.5 unit change in both x and y, so the boundary conditions are fairly easy to set up:
Now comes the mathy-goodness. The next step is to discretize the equation. This is where the math comes in and is a little bit more complicated than I can do a good job explaining. The required background information can be found on Wikipedia. Suffice it to say that from this, we find that the value at each point inside our domain is approximately equal to the average of the points in each cardinal direction. Put mathematically, we have:
 |
| Note: i index indicates position on x-axis, j index indicates position on y-axis |
The final step is to make it a little easier to see what's happening. I started by adding color using the conditional formatting color scale option:
This is pretty cool and gives a pretty good idea of what's going on. Another option is using the 3-dimensional graph:
If you've been following this, you're probably thinking this is pretty good. I am always surprised by the things you can get Excel to do if you want. If you haven't been following this but have still made it to the bottom of the post, I'm glad you stuck with it to the end but I apologize for an ending that's probably pretty disappointing. The posts after this one deserve some less intellectual content and I intend to deliver.
-Lane
Saturday, June 4, 2011
Math, The Way it Should Be (Unit 1.5: Number Lines, Planes, and Vectors)
It’s been a bit of time since the last math post. Hopefully you’ve used the time to review the previous lessons and done all your homework.
As always, the start of the series is here and the start of the unit is here. This lesson doesn’t have very much new notation, either. I think that later units will have more new notation. This lesson is about looking at numbers in a more visual way and sets up the entirety of the next unit.
Here, you can see the integers between -5 and 5 and the arrow heads indicate that the numbers continue in either direction. The line may be marked at any interval. For example, if I had wanted, I could have put only even numbers on the line and the number line would have been equally legitimate. This can be a very useful way of thinking about numbers and the things we do with them. Addition can be thought of as movement to the right along the line, while subtraction is movement to the left. To explain multiplication in a similar way, I need to introduce something called a vector.
A vector is commonly described as a magnitude and a direction. In other words, it is an arrow with a known length and we know which way it points. On the number line, the vector starts from zero and points to the number which corresponds to its length. A vector representing the number two looks like this:
To multiply by two, we simply double the length of the arrow:
We get the expected result, which is four. I feel like this is a much better way of imagining multiplication, rather than the rows/columns method presented earlier. Division can be described in a similar way: instead of doubling the length of the arrow to multiply by two, you halve the length of the arrow to divide by two.
These two lines can represent anything, especially things that can’t be compared, like apples and oranges. One line would represent apples, and the other oranges, and any combination of apples and oranges could be represented by a place on this “plane”. The number lines are now called axes. For example, if you have two apples and three oranges:
A vector could be drawn to this location (from the point representing a person having no apples and no oranges). In either case, the point where you are with your fruit and the vector pointing to you are represented by (2,3).
The two red vectors are your apple vector (2,0) and your orange vector (0,3) and they add to your fruit vector (2,3). BAM! You just learned vector addition. When adding two vectors, you simply add their components. If I have one orange and three apples (3,1) and give them to you (2,3), you will move to (5,4). Vector subtraction is similar. If you eat two apples and two oranges, you go down two on the orange axis and to the left two on the apple axis to (3,2). Keep this in mind.
Homework:
- Review your times tables. I'm not kidding, they really are that important.
- Draw a Cartesian plane and label the axes. Label the vertical axis something made-up, like unicorns and the horizontal axis something real, like fire trucks. Imagine yourself somewhere on this plane with at least one unicorn. This is also important, as you will see later.
-Lane
Thursday, May 26, 2011
Math, The Way It Should Be (Unit 1.4: Numbers, Part 4)
If you haven’t seen this series before, you should start here or here. The last lesson covered rational numbers and how to solve equations involving multiplication and addition. It also introduced another type of problem, those involving exponents. Exponents, generally speaking, indicate multiple instances of multiplication. In other words,
52 = 5·5 = 25
53 = 5·5·5 = 125
It continues on like this for all integers and rational numbers. The problem is when you want to go in the other direction. To do this, you have to use an operation called a root. The square root of x looks like this:For equations like the one below, it is easy to find the solution of using a square root. You just have to keep one thing in mind: a square root generates two answers, a negative and a positive answer. This is because you are doing the opposite of multiplying two numbers together and the product of two negative numbers is positive.
The answer in this case is either 5 or -5! If you check this result, you will find that squaring either number results in 25. There are two problems with the square root, and they come when you encounter two different numbers.
Now we can solve equations involving exponents with all positive numbers. But what happens if we want to take the square root of a negative number? I already said that the product of two positive or negative numbers is always positive. So how do you choose a number that, when multiplied by itself, is equal to a negative number? We introduce a new set of numbers, the imaginary numbers. I’m not kidding. That’s what they’re actually called and the most important imaginary number is i. i is the square root of -1. This allows us to factor negative numbers into -1 and a positive number. We then take the square root of the positive number and multiply by i:
Don’t forget that there are still two answers! When combined with the real numbers (integers, rational and irrational numbers), the imaginary numbers form the complex plane. A complex number is one that is the sum or difference of a real number and an imaginary number. Much farther down the line, we’ll see why it’s called the complex plane, but suffice it to say that it’s called that as a result of the complex plane not being an ordered set. Now we’ve talked about all of the relevant numbers. We can solve equations involving addition, subtraction, multiplication, division, and exponents for all real and imaginary numbers!
Homework: as long as you’ve followed this lesson, I’m happy. For the advanced student, the following exercises can be enlightening:
- Prove the square root of two is irrational (hint, recall the definition of rational and prove by contradiction)
- Prove that the complex plane isn't an ordered set (hint, recall the properties of an ordered set and prove by contradiction)
-Lane
Monday, May 23, 2011
Math, the Way it Should Be (Unit 1.3: Numbers, Part 3)
Not related to math, but today is my five year anniversary with my fiancée! I'm so excited to spend the day with her!
As always, the start of the series is here and the start of the unit is here. When we left off last, we had just talked about all of the integers. We had learned to solve algebra problems involving addition, subtraction, multiplication, and some instances of division. But we ran into a problem with division: sometimes we can’t split an integer number of objects into an integer number of groups, each with the same integer number of objects. In the example last time, we had twelve objects we wanted to put into 5 groups and we couldn't find an integer that worked.
What’s the solution? Come up with a new set of numbers. In this case, we use the rational numbers. The rational numbers are characterized by the ability to be written as the ratio of two integers. That is, the answer to our 12 objects in 5 groups is 12/5 or x, the number of objects in each group is 12/5:As always, the start of the series is here and the start of the unit is here. When we left off last, we had just talked about all of the integers. We had learned to solve algebra problems involving addition, subtraction, multiplication, and some instances of division. But we ran into a problem with division: sometimes we can’t split an integer number of objects into an integer number of groups, each with the same integer number of objects. In the example last time, we had twelve objects we wanted to put into 5 groups and we couldn't find an integer that worked.
This is also the solution to the equation:
5x = 12
This set of numbers looks like fractions, but please don’t start hyperventilating until the end of the lesson. Some things to take note of about the rational numbers:
- All of the integers are already rational numbers (think of them being divided by one: 5/1 = 5)
- The rational numbers are an ordered set (5/3 < 5)
- The rational numbers are the first group of numbers that are said to be “dense”.
Density is a pretty cool property for a group of numbers to have. In essence, it means between any two rational numbers, there are an infinite number of rational numbers. Why am I just bringing this awesome property up now? I haven’t mentioned it yet because the counting numbers and the integers are not dense. Let’s look at an example. If we think about two integers, say 3 and 7, we can see exactly how many integers are between them (we can do this because the integers are an ordered set). We have 4, 5, and 6. There are a finite (three) number of integers between 3 and 7. Now let’s look at the rational numbers between 3 and 7. We still have 4, 5, and 6, but we also have 7/2, 9/2, 11/2, 13/2, 13/3, 14/3, 16/3, 17/3, 19/3, 20/3… and the list goes on forever.
Hold off on the hyperventilation for a bit longer while we delve into decimals. Decimals are a special way of representing numbers and involve the addition of fractions. Say for instance, we have the number 3.7. This number in the ones’ place indicates how many whole objects we have, in this case, three. The next number after the decimal place indicates how many tenths we have (seven). So this number is the same as 3 + (7/10). Now we can change the way the number 3 looks by multiplying by a funny-looking version of the number one. You would agree that if you put 10 objects evenly into 10 groups, you would have one object in each group, right? So 10/10 is equal to 1. Now to multiply two fractions, you multiply their top numbers and multiply their bottom numbers like so:
This is a great result! We have changed the way the number 3 looks without changing its value! Now we can add 3 and 0.7. To add fractions, you make sure their bottom number is the same (in this case, 10) and then add their top numbers:
And all of a sudden, decimals are demystified. We can see from the above result that because 3.7 can be written as the ratio of two integers, it is a rational number.
I personally prefer fractions and like to avoid decimals because sometimes decimals can only reasonably approximate an actual number. Take 1/3 for example. There it is in a simple fraction, for all the world to see. We can imagine exactly what it is: one-third. But try writing it as a decimal and you get 0.333333333333… and the threes just keep coming! You can write it, but only with an infinite number of threes. This is why I typically don’t deal in decimals. I also avoid percentages because they are stupid: simply take the decimal and multiply by 100. So I have good news for you, if fractions, decimals, and percentages give you pain: I won’t be dealing in either of the last two things. Just remember that to add fractions you make the bottoms the same (by multiplying by 1) and then add the tops and to multiply two fractions you multiply the tops and the bottoms.
Now to solve a problem requiring division:
5x = 12
(5x)/5 = 12/5
1x = 12/5
x = 12/5
Using rational numbers, we can now solve any multiplication or division problem. The next problem we need to solve looks like this: x2 = 5. That requires two new types of numbers, but after that, we’re done and will be moving on! One other thing to remember about multiplying and dividing with negative numbers: if you combine two negative numbers or two positive numbers, you get a positive number. If you combine one of each, you get a negative number.Homework:
- Practice adding and multiplying fractions.
- I should have said this before, but throw away your calculator. It is a crutch that makes you rely on decimals.
- Forget about degrees. The better you do this, the better future lessons will go. Start now, though, because it will be harder than you think.
-Lane
Tuesday, May 17, 2011
Math, The Way It Should Be (Unit 1.2: Numbers, Part 2)
This the second part of the first unit on numbers. If you want to start at the beginning of the unit, go here. If you want to start at the very beginning, go here. This lesson doesn't contain any new symbols but does have a lot of vocab.
Recall that we started with the counting numbers (1, 2, 3, ...). These are your very basic numbers, the first we encounter in our education, and this re-education is no different. Next, we include the number 0 (which represents nothing) to the set. This is a fairly big step that took human civilization thousands of years. It is important because it is the "additive identity", in that zero added to any number results in that number. After that, we include negative numbers, which are less than zero. They mirror the counting numbers and are referred to as their opposites. For example, the opposite of 4 is -4. The interesting thing about two opposite numbers is that their sum is always zero. This leads to the realization that subtraction is really just the addition of a number and the opposite of another number:
4 - 4 = 4 + (-4) = 0
The set that includes the counting numbers, their opposites, and zero is called "the integers". You may convince yourself that the integers are an ordered set. Now everyone is happy. We can effectively solve algebra problems that involve addition and subtraction. For example:
x + 4 = 5
x + 4 + (-4) = 5 + (-4)
x + 0 = 1
x = 1
Ta dah! An algebra problem is solved. Don't be frightened by the unknown variable. It is easy to find once you know how. To eliminate the number that accompanies the variable, you add it's opposite. Since the sum of a number and its opposite is zero and zero is the additive identity, you are left with only the unknown variable. Of course, you must do the same thing on the other side, since you can't change one side and not the other and still have them be equal.
Side note: any variable can be used instead of x. One of my math teachers was especially fond of "dead dog" and "house". This flexibility will be useful later.
Now for multiplication and division. I feel like these operations are poorly understood and difficult to explain. Multiplication can best be thought of in terms of rectangles. Imagine a square with side length equal to 1. The following expression:
3 x 4
Can best be thought of as a rectangle containing 3 of these squares on a side and 4 on the other, like this:
Count the number of squares. You'll find there are 12, a result that you should have expected. This can be alternately be represented in the following ways:
3(4) = 12
3·4 = 12
3 x 4 = 12
3*4 = 12
Only the first two are commonly used, so forget about using the third one. The fourth is used in computer applications because the asterisk is on the keyboard. Don't hand-write that one. An important property to point out is that 1 is the multiplicative identity, that is, that one multiplied by any number results in that number.
Imagine now that you have 12 boxes in the above configuration. If you want them put in three groups. You would find that evenly split up, there are four in each group. This is represented in the following ways:
12 ÷ 3 = 4
12/3 = 4
The twelve may also be put directly over the 3 in the second case (this is the most commonly seen). Don't write the first one. It makes you look like an amateur. One is also unique in division: divide any number by one and you will have the number you started with. Also, never divide by zero. Mathematicians don't agree on what happens when you do this, but it's always bad.
What if you want to put your 12 boxes in five groups? There is no integer that can result from putting 12 objects evenly in 5 groups. We will need a new kind of numbers to solve the following equation:
That is the subject of another lesson. I hope by now that you see that I am presenting new groups of numbers as the solution to new kinds of problems. Counting numbers are required to count. Integers are required to do addition, subtraction, multiplication, and some division. But not all division can be done this way. The next lesson on numbers will cover these numbers.
One last thing to take note of: adding and multiplication can be done in any order (for now). Subtraction and division are best done in the order they're written in.
1 + 2 = 2 + 1
2 - 1 ≠ 1 - 2
Homework:
- Learn your "times tables". No joke. They're important and will come in handy later.
- Forget that you ever saw this: ÷
- Never, ever again say "times it by" in reference to multiplication. To say something like "to do multiplication, one simply takes the first number and times it by the second" is wrong. Not only is it incorrect, but it's against the morals and ethics of society. Most importantly, it makes my blood boil.
-Lane
Sunday, May 15, 2011
Math, The Way It Should Be (Unit 1.1: Numbers, Part 1)
This is the first lesson of the first real unit in the "Math, The Way It Should Be" series. If you missed why this is happening, you should look here. This post is going to cover some basics about numbers and the way we write them and some of the things that we do with them. Again, don't skip this section, even if you think you have a pretty good handle on numbers (even though you probably do).
Each lesson will begin with an explanation of the symbols that you will need to know to get the lesson off the ground. The symbols that we are going to need right now are as follows:
Each lesson will begin with an explanation of the symbols that you will need to know to get the lesson off the ground. The symbols that we are going to need right now are as follows:
Now I know that you've seen these before and I'm not trying to be a wise-ass. They are very important and I'm including them here for completeness and I want everyone to be on the same page as I am. They are, in order: equal to, less than, greater than, less than or equal to, and greater than or equal to. The first symbol means that the objects on both sides have same value (value to be discussed later). The second symbol means that the object on the left has a smaller value than the object on the right. The third symbol means that the object on the left has a greater value than the object on the left. The fourth and fifth symbols indicate the same thing as the second and third, except that they also admit the possibility that the two objects have the same value.
Now that we know what the symbols are, let's talk about some numbers. Numbers are essentially symbols that have certain values that we all agree on. The first type of numbers are the first ones that you learn: 1, 2, 3, 4, etc. They are called the counting numbers and refer to a set (or group) of numbers that one uses to count things. If you have one duck and then get another and count your ducks, you have 2 ducks.
When you learn about new groups of numbers, it's nice to think about what properties the group has. One nice thing about this group is that it's an "ordered set" meaning that if you take two of the objects, you can say one of three things:
- The first object is greater than the second object (4 > 2)
- The first object is less than the second object (4 < 6)
- The first object has the same value as the second object (4 = 4)
This is an extremely useful property because it allows us to count, which is the whole point of these numbers. From this set comes two very useful things to do with numbers: addition, subtraction.
Addition is the combination of two or more objects to create a collection of objects. We use the + sign to indicate this type of combination. Returning to the duck example, you had one duck and got another duck and ended up with two ducks. This is written as 1 + 1 = 2. Subtraction is the removal of one object from a collection of objects. We use the - sign to indicate this process. This symbol comes up again in a very interesting way later. You eat one of your ducks and now you have one*. This is written as 2 - 1 = 1.
As this is the first lesson and I hope that everyone has a pretty good handle on this material, if you're happy with the pace, there is no homework. If you feel that I am insulting your intelligence, I encourage you to leave a rigorous, mathematical proof that 1 + 1 is always equal to 2 in the comments.
-Lane
*No ducks were harmed in the making of this post.
Saturday, May 7, 2011
Math, The Way It Should Be (Unit 0: The Beginning)
I have encountered many people who are not good at math. There are a number of reasons for this, many of them perfectly legitimate. Perhaps learning more math never seemed useful, perhaps a teacher wasn't able to explain fractions very well and things went downhill from there. My intention at this point is to start at the very beginning (waaaaay at the beginning) because I firmly believe that a lack of foundation is the root of many people's trouble with mathematics.
Why am I doing this? Reason number 1: math is part of the way I look at the world. At a sufficiently high level, the math becomes a beautiful expression of the way the world works. If the universe were an Italian opera, mathematics is Italian. You can enjoy it without the language, but there is something rewarding to me about getting as much of the full story as possible. Reason number 2: math is surprising useful. All it takes is a little creativity in application and all of a sudden you're making things a lot easier!
Right now, I estimate that there are going to be 12 units, each with multiple parts (this introductory post doesn't count as a unit). This is not intended to replace education, but if you've stopped where you left off, hopefully I can give you a little more understanding. Don't skip topics, they're very important because I'm going to go in the order that makes the most sense after looking back on my own mathematics education. That leads me to my next point: this series of posts is dedicated to the people who made me the mathematician I am today: Mrs. Peck, Mrs. Wells, Ms. Graves, Mr. Atherton, Mr. Alexander, Mr. McGowan, Mr. Anthony, Professor Volkov, Professor Humi, Professor Mosco, and Professor Mitrea.
One last thing: there will be homework, but it won't be collected for credit. This week's assignment: brush up on your times tables. If this is the only thing you get out of this series, it will have been completely worth it.
-Lane
Subscribe to:
Posts (Atom)